How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Chinese missile could shift Pacific power balance
- Thread starter Lankan Ranger
- Start date
lcloo
SENIOR MEMBER

- Joined
- Jul 28, 2010
- Messages
- 3,981
- Reaction score
- 14
- Country
- Location
IF
Third...I have seen the inside of an AIM-7 and AIM-9. Both are hollow tubes, albeit very robustly constructed for high-G maneuvers.
So yes, my calling an ICBM a 'hollow tube' is technically and contextually correct.
Flying hollow tubes, ha, ha, I like that.

Thomas
PROFESSIONAL

- Joined
- Jul 22, 2009
- Messages
- 2,688
- Reaction score
- 0
You'd better tell that to someone who thinks that once the missile enters a turn then its trajectory is determined and predictable.
your confusing that I said "it can be tracked from launch", with knowing at launched where it's going to hit. I never said that once it is launched we would know it's impact point. I said we can track the missile. And if your above statement is true then what you are saying is that the Aegis BMD, and SM-2/3 missiles do not work as advertised. Since they rely on being able to determine just that in order to achieve a kill.
IF you did know it, you would know that a 'gravity turn' is essentially a zero angle of attack maneuver...
Gravity turn - Wikipedia, the free encyclopedia
A gravity turn is performed usually endoatmospheric. If there is zero angle of attack, then we can estimate the vehicle to be orbital at some point. The moment there is a change in angle of attack AFTER the the vehicle entered the maneuver, and we know that gravity pulls the vehicle towards Earth, then we can recalculate the vehicle's path based upon that point of change to where it might be pointing at on the ground.
You are more miserable than I imagined.
Of course its AoA is zero if it is an ideal gravity turn. I doubt you even understand what AoA means in this matter. However even with an ideal gravity turn, the vector velocity of missile trajectory is still determined by the duration of the boost phrase when rocket is firing. To put in simple physics, the state of the missile is determined by the sum of forces act on it during its flight. During the boost phase of the ballistic missile's flight, three forces act on the missile, gravity drag, aerodynamic drag and propulsion from thrust . Now, gravity drag, and aerodynamic drag can be more or less predetermined, however the flux of thrust during the boost phase is an unknown variable until the rocket finishes producing thrust. The trajectory of the missile can not be calculated until all the variables are known, that is simple math. It seems that you are the one who is putting those parameters into the missile before every launch. If I can post attachment here I would draw you a graph to show how different durations of boost phase affect the burnout vector velocity and attitude of a missile and how different vector velocity and attitude affect missile's trajectory even if it is an ideal gravity turn.
Obviously you have mistaken boost phase for ascending phase.
Besides not all the missile has to follow an ideal gravity turn for its trajectory during its boost phase, that is why it is called ideal gravity turn.

Thrust_vectoring#Rockets_and_Missiles
The word 'even' implies an option, meaning you are implying that an ICBM has the option of entering that maneuver. Wrong. An ICBM has no choice but to enter the gravity turn. The better phrasing should be 'Once the missile enters the gravity turn...'
Okay, let me rephrase it into what I want to say.
Once the missile enters the gravity turn and even if it stay with its course(which mean the rocket does not use thrust to steer its direction, thus AoA is 0) the trajectory of the missile still need to be determined after the rocket burns out(end of the boost phase), because only after the rocket burns out, the missile enters its mid-course phase coasting through space before reentering the atmosphere in a predictable parabola manner., Here again from your own wiki source.
The duration of rocket producing thrust is not a constant, it can be programed to vary for each launch. For a liquid fuel rocket, the amount of fuel added before its launch determines the duration of its firing time. For multi stage missiles, the ignition of second and third stages can be delayed with solid fuel rockets.Wrong as shown above with the gravity turn being low or zero angle of attack. When including constant thrust then it is eminently possible to predict a ballistic flight path.
Man...oh...man...No wonder you guys are so entertaining...Perhaps you mean 'phases'?
Anyway...The problem for endoatmospheric multistagings is the ignition timings between stages.
For example...
See that empty space on the Soyuz's body and below orange/yellow area? That is the 'interstage' portion. We found out a long time ago that for the most in multistaging operation, there are problems associated with interstage ignition and the type of fuel. If the vehicle is liquid fueled, the tanks are not completely full to allow for fuel expansion but potentially the fuel may not be on the bottom of the tank, so there might not be proper sequential stage ignition. So we created 'ullage' rockets...
That is only a problem for liquid fuel rockets, most of the modern ballistic missiles all use solid fuel as their propellant, which uses different method for ignition.
For solid fuel the multistaging ignition timing is still there except that even though we do not need ullage motors, solid fuel do not ignite as rapidly as liquid fuel can, so what we do is called 'hot staging' where the next stage engine is lit in very precisely controlled manner BEFORE separation. The lower or previous stage section is heavily shielded with fire retardant material so it would not catch fire and possibly explode.
The above is an illustration of the Minuteman multistaged ICBM. Look at timestamp 2:46 when the lower stage is separated and when the upper stage is already lit, maintaining constant thrust.
So for you to say this: '...coasting period between the two stages...' is absolutely incorrect for someone who claimed to majored in aeronautical engineering. The difference between 'stage' and 'phase' is not allowed for such an education. The only time there is any 'coasting' between stages is when the vehicle is ALREADY in orbit and the final stage is ignited to send the bus into the descent. Even then, it should be properly phrased as 'phase' because the vehicle's location -- orbit -- take precedent in description.
Just for this Minuteman's demonstration the multistaging ignition is this way, it doesn't mean it has to be like this all time. Some missiles or even rockets are designed to call for extra free-flight time between stages.
The amount of thrust to send the vehicle into a gravity turn is: ZERO = 0.
Only if it is an ideal gravity turn.
Gravity turn - Wikipedia, the free encyclopediaAfter the pitch over is complete the engines are reset to point straight down the axis of the rocket again. This small steering maneuver is the only time during an ideal gravity turn ascent that thrust must be used for purposes of steering.
Absolutely.
First...The fact that you differentiate 'rocket' and 'missile' here tells me you really do not know what you are talking about. The difference between a 'rocket' and a 'missile' is more contextual than technical. A 'missile' has a sensor/guidance system. A 'rocket' does not. But a 'rocket' is also a description for a vehicle that uses mainly directed thrust instead of aerodynamic exploitation for flight. That mean a 'rocket' is also the basis for a 'missile'. A satellite launcher is a 'missile' because it has a sensor/guidance system and that it has a specific target or spatial location in its electronic mind.
Second...If we go back to the 'gravity turn' wiki source again, we would find this bit...

Your gravity turn wiki source never mentions missile at all.
Do you ever wonder why missiles mainly use solid fuel as its propullent besides cutting the preparation time short even though liquid fuel provides higher thrust. Your knowledge is fixated on first generation missiles where it is more or less the same with commercial rockets.
Commercial rockets are not designed to endure high stress manuvers that modern missiles have to withstand.
A lot of the information I used to clean your BS is from your own wiki source of "gravity turn".In your dream.
Last edited:
your confusing that I said "it can be tracked from launch", with knowing at launched where it's going to hit. I never said that once it is launched we would know it's impact point. I said we can track the missile. And if your above statement is true then what you are saying is that the Aegis BMD, and SM-2/3 missiles do not work as advertised. Since they rely on being able to determine just that in order to achieve a kill.
I agree with what you have said about tracking the missile after launch. My point is that you can only determine the destination of its target after all the variables in calculating its trajectory are known after it exits the boosting phase.
Last edited:
gambit
PROFESSIONAL

- Joined
- Apr 28, 2009
- Messages
- 28,575
- Reaction score
- 148
- Country
- Location
Heh...heh...heh...

'For ballistic missile unless it is aimed at its maximum range, the amount of thrust used for steering the missile is still an unknown variable to outside observers.'
There is no changing of thrust to enter that maneuver. There is a redirection of the main engines. You are getting desperate, friend, enough to start making nonsensical arguments.
Gravity turn - Wikipedia, the free encyclopedia
Correct...Only in your imagination that I am 'miserable'.You are more miserable than I imagined.
I understand angle-of-attack better than you do. And please show the readership an example of a 'non-ideal gravity turn'. This I have got to see.Of course its AoA is zero if it is an ideal gravity turn. I doubt you even understand what AoA means in this matter.

Then all you have to do is show us a source that says so. If what you say is true, then interception even by car to another car is not possible. Pure pursuit navigation by a missile in tail chase condition is not possible. This is truly 'Chinese physics' we are seeing here.However even with an ideal gravity turn, the vector velocity of missile trajectory is still determined by the duration of the boost phrase when rocket is firing. To put in simple physics, the state of the missile is determined by the sum of forces act on it during its flight. During the boost phase of the ballistic missile's flight, three forces act on the missile, gravity drag, aerodynamic drag and propulsion from thrust . Now, gravity drag, and aerodynamic drag can be more or less predetermined, however the flux of thrust during the boost phase is an unknown variable until the rocket finishes producing thrust. The trajectory of the missile can not be calculated until all the variables is known, that is simple math. If I can post attachment here I would draw you a graph to show how different durations of boost phase affect the burnout vector velocity and attitude of a missile and how different vector velocity and attitude affect missile's trajectory even if it is an ideal gravity turn.
We are talking about the boost phase. Granted, there is greater variability in predicting the final so early in the flight, but that still does not prevent us from making path projections.Obviously you have mistaken boost phase for ascending phase.
Then all you have to do is show us an example of a 'non-ideal' one. Your previous claim is this:Besides not all the missile has to follow an ideal gravity turn for its trajectory during its boost phase, that is why it is called ideal gravity turn.
'For ballistic missile unless it is aimed at its maximum range, the amount of thrust used for steering the missile is still an unknown variable to outside observers.'
There is no changing of thrust to enter that maneuver. There is a redirection of the main engines. You are getting desperate, friend, enough to start making nonsensical arguments.
That still does not prove that flight path estimation is impossible.Okay, let me rephrase it into what I want to say.
Constant thrust here is force, not duration. Failure to understand this show you do not know what you are talking about.The duration of rocket producing thrust is not a constant, it can be programed to vary for each launch. For a liquid fuel rocket, the amount of fuel added before its launch determines the duration of its firing time. For multi stage missiles, the ignition of second and third stages can be delayed with solid fuel rockets.
The point was to show that you are wrong about 'coasting' between stages. For a two-stage missile, the upper stage is for orbit, then coast until reentry. Now...If you can show that the DF-21 is SSTO, then you may have a point. Until then...You are wrong.That is only a problem for liquid fuel rockets, most of the modern ballistic missiles all use solid fuel as their propellant, which uses different method for ignition.
Just for this Minuteman's demonstration the multistaging ignition is this way, it doesn't mean it has to be like this all time. Some missiles or even rockets are designed to call for extra free-flight time between stages.
Sure it does...Your gravity turn wiki source never mentions missile at all.
Gravity turn - Wikipedia, the free encyclopedia
As you can see, just about every rocket-type vehicle engages in a gravity turn, in which the vehicle's flight path can be predicted.Guidance and control
The steering of a rocket's course during its flight is divided into two separate components; control, the ability to point the rocket in a desired direction, and guidance, the determination of what direction a rocket should be pointed to reach a given target. The desired target can either be a location on the ground, as in the case of a ballistic missile, or a particular orbit, as in the case of a launch vehicle.
Ballistic missiles do not maneuver like air-air missiles so this 'commercial' versus 'missile' argument is nonsense.Do you ever wonder why missiles mainly use solid fuel as its propullent besides cutting the preparation time short even though liquid fuel provides higher thrust. Your knowledge is fixated on first generation missiles where it is more or less the same with commercial rockets.
Commercial rockets are not designed to endure high stress manuvers that modern missiles have to withstand.
The only thing you did was produced more BS, which I just cleaned up.A lot of the information I used to clean your BS is from your own wiki source of "gravity turn".
gambit
PROFESSIONAL

- Joined
- Apr 28, 2009
- Messages
- 28,575
- Reaction score
- 148
- Country
- Location
No one said anything about certainty of ground target. We are saying that for each phase of an ICBM flight, we can make projections on where it is going to be, and assuming no changes we can predict a ground point. If we know there is a valuable target like an air force base and nothing else around for a couple hundreds klicks, what else can that ground point be?I agree with what you have said about tracking the missile after launch. My point is that you can only determine the destination of its target after all the variables in calculating its trajectory are known after it exits the boosting phase.

The further back we move towards the missile's launch point, we are effectively moving our detection and interception capability towards the enemy. Right now we have terminal defense and are working on the rest. But for every segment or phase of the missile's flight, as long as we are able to detect and track, we can make path projections.
Heh...heh...heh...
Correct...Only in your imagination that I am 'miserable'.
I understand angle-of-attack better than you do. And please show the readership an example of a 'non-ideal gravity turn'. This I have got to see.
Easy, any time that the thrust is used to produce an angular acceleration either upward or downward to change missile's direction will be considered as a non ideal gravity turn.
Tell me how SS-27 Topol-M is able to fly relatively flat ballistic trajectory using ideal gravity turn then.
http://www.armscontrol.org/act/2000_06/topoljun
Then all you have to do is show us a source that says so. If what you say is true, then interception even by car to another car is not possible. Pure pursuit navigation by a missile in tail chase condition is not possible. This is truly 'Chinese physics' we are seeing here.
It seems that the car you are trying to pursuit is in an straight line without any change of speed and direction. In real life, the driver can steer the car any direction he wants during the pursuit, and the intercepting car needs to adjust its heading for any change of circumstance of target car. Those changes includes acceleration, deceleration and steering to any directions. Let's put into the simple prospective here without involving the complexity of steering. Car B is to intercept Car A, and there are two phases of the movement of Car A, an acceleration phase and a deceleration phase. To make things easier, let's say the acceleration "a" and deceleration "d" are constant and Car A starts from 0 speed. The only variable here is actually the time "t1" of its acceleration. So the speed "v" of at end of its acceleration is v=a*t1, and the distance "D1" it has traveled during this phase is D1=1/2 *a*t1^2. Only from there we can calculate the time "t2" before Car A comes into a completely stop due to the deceleration force from frictions. 0-v=-dt2, t2 = v/d = (a*t1)/d, and the distance "D2" during the second phase is D2 = 1/2*d*t2^2 = 1/2*d*[(a*t1)^2/(d^2)] =1/2 *(a*t1)^2/d.
So the total distance the car A will travel D = 1/2 *a*t1^2 + 1/2 *(a*t1)^2/d.
So in order for car B to intercept the car A, we need to know the exact distance it has traveled in relationship to the time from its original position.
The function D(t) is
1.D(t) = 1/2 * a * t^2, if 0 <= t <= t1
2.D(t) = 1/2 * a * t1^2 + [v(t-t1) - 1/2*d*(t-t1)^2]
= 1/2 * a * t1^2 + [a*t1(t-t1) -1/2 * d * (t-t1)^2] if t1 < t <= (a/d + 1) * t1
Now if you want to know where to intercept Car A during its deceleration phase, it is impossible to know where the location at any given time it is without knowing the t1 which is the time of its acceleration period. Without knowing t1, you can still intercept Car A if both car are heading towards each other in a straight line, but you still will not know the exactly location alone the straight line of interception. I guess they did not teach that in Vietnamese physics.
Without knowing the duration of the thrust, how do you know the net momentum the propulsion has transfered to the missile. You lack the basic understanding of simple physics.Constant thrust here is force, not duration. Failure to understand this show you do not know what you are talking about.
Ha, that is a first. You again use space rocket principles applying to missile. That shows how much you know about missile. Since when does a missile has to enter a planetary orbit with the exception of maybe X-43A???The point was to show that you are wrong about 'coasting' between stages. For a two-stage missile, the upper stage is for orbit, then coast until reentry. Now...If you can show that the DF-21 is SSTO, then you may have a point. Until then...You are wrong.
There are a few common ways of understanding orbits.
As the object moves sideways, it falls toward the central body. However, it moves so quickly that the central body will curve away beneath it.
A force, such as gravity, pulls the object into a curved path as it attempts to fly off in a straight line.
As the object moves sideways (tangentially), it falls toward the central body. However, it has enough tangential velocity to miss the orbited object, and will continue falling indefinitely. This understanding is particularly useful for mathematical analysis, because the object's motion can be described as the sum of the three one-dimensional coordinates oscillating around a gravitational center.
I am not saying it has to maneuver like AAM, but it definitely is more maneuverable than commercial rockets. By using solid fuel the diameter of the rocket body is greatly reduced, thus the casting is more stress resisting as comparing to commercial liquid fuel rockets if their casting are made of the same material and the width of the casting wall are the same.Ballistic missiles do not maneuver like air-air missiles so this 'commercial' versus 'missile' argument is nonsense.
σc is Hoop Stress and σr is Radial Stress
σc = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] - {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
σr = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] + {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
Everything is BS according to your "Vietnamese physics"The only thing you did was produced more BS, which I just cleaned up.
Sorry, you are.No one said anything about certainty of ground target. We are saying that for each phase of an ICBM flight, we can make projections on where it is going to be, and assuming no changes we can predict a ground point. If we know there is a valuable target like an air force base and nothing else around for a couple hundreds klicks, what else can that ground point be?
Sure we know where it is going to be, on EARTH, and probably know which side of earth too.
Oh, really, I thought according to you there can not be any changes during its boost phase.
Last edited:
gambit
PROFESSIONAL

- Joined
- Apr 28, 2009
- Messages
- 28,575
- Reaction score
- 148
- Country
- Location
It is 'Easy' because you made it up. I asked for an example, not your interpretation.And please show the readership an example of a 'non-ideal gravity turn'. This I have got to see. Easy, any time that the thrust is used to produce an angular acceleration either upward or downward to change missile's direction will be considered as a non ideal gravity turn.
Easy, any time that the thrust is used to produce an angular acceleration either upward or downward to change missile's direction will be considered as a non ideal gravity turn.
Tell me how SS-27 Topol-M is able to fly relatively flat ballistic trajectory using ideal gravity turn then.
Russia Approves Topol-M; Warns Missile Could Defeat U.S. Defense | Arms Control Association
ICBMs and satellite launchers are alike during the initial rise out of the lower atmosphere. But because a ballistic trajectory is primarily for ground coverage a 'ballistic missile' is a vehicle that continues on a path that must includes more of Earth's gravity than a satellite launcher would.
In this phrasing:
'After the pitch over is complete the engines are reset to point straight down the axis of the rocket again. This small steering maneuver is the only time during an ideal gravity turn ascent that thrust must be used for purposes of steering.'
A redirection of thrust is initiated to induce a pitch over. The angle and duration of that redirection produce the desired ground coverage. Once the pitch over, which is an angle-of-attack change, is completed and the missile is on the desired heading and in the 'gravity turn' maneuver, thrust is redirected again back to longitudinal alignment, which is another angle-of-attack change in itself. All the while gravity exerts a persistent pull on the entire vehicle.
The word 'ascent' is important because we are trying to send the bus into orbit. The 'ascent' subphase is after the 'boost' phase, which is followed by the mid-course (orbit) phase. The entire phrasing mean that a 'gravity turn' is the ideal maneuver to achieve that ground coverage via ascension to orbit. It also mean ANY gravity turn is an 'ideal gravity turn' regardless if there are any angle-of-attack changes while inside the maneuver.
Nice figures but I asked for a source to your claim that target path projections are impossible. Anyone can hack up any math to support his argument and in this publicly accessible forum, the laymen can be misled by non-sourced comments.It seems that the car you are trying to pursuit is in an straight line without any change of speed and direction. In real life, the driver can steer the car any direction he wants during the pursuit, and the intercepting car needs to adjust its heading for any change of circumstance of target car. Those changes includes acceleration, deceleration and steering to any directions. Let's put into the simple prospective here without involving the complexity of steering. Car B is to intercept Car A, and there are two phases of the movement of Car A, an acceleration phase and a deceleration phase. To make things easier, let's say the acceleration "a" and deceleration "d" are constant and Car A starts from 0 speed. The only variable here is actually the time "t1" of its acceleration. So the speed "v" of at end of its acceleration is v=a*t1, and the distance "D1" it has traveled during this phase is D1=1/2 *a*t1^2. Only from there we can calculate the time "t2" before Car A comes into a completely stop due to the deceleration force from frictions. 0-v=-dt2, t2 = v/d = (a*t1)/d, and the distance "D2" during the second phase is D2 = 1/2*d*t2^2 = 1/2*d*[(a*t1)^2/(d^2)] =1/2 *(a*t1)^2/d.
So the total distance the car A will travel D = 1/2 *a*t1^2 + 1/2 *(a*t1)^2/d.
So in order for car B to intercept the car A, we need to know the exact distance it has traveled in relationship to the time from its original position.
The function D(t) is
1.D(t) = 1/2 * a * t^2, if 0 <= t <= t1
2.D(t) = 1/2 * a * t1^2 + [v(t-t1) - 1/2*d*(t-t1)^2]
= 1/2 * a * t1^2 + [a*t1(t-t1) -1/2 * d * (t-t1)^2] if t1 < t <= (a/d + 1) * t1
Now if you want to know where to intercept Car A during its deceleration phase, it is impossible to know where the location at any given time it is without knowing the t1 which is the time of its acceleration period. Without knowing t1, you can still intercept Car A if both car are heading towards each other in a straight line, but you still will not know the exactly location alone the straight line of interception. I guess they did not teach that in Vietnamese physics.
Without knowing the duration of the thrust, how do you know the net momentum the propulsion has transfered to the missile. You lack the basic understanding of simple physics.

Assume the bogey at the time of detection (contact) remain unchanged in this flight, in fixed coordinate system, his would be (Vt,D) where V is the bogey's speed, t is detection time and D is distance between fighter and bogey. Give the fighter's speed as F. Its coordinates would be (Ftsin(h), Ftcos(h)) where h is heading and angle relative to the estimated bogey's flight path. Give the missile's speed as M and substitute for F. Maritime history is full of collisions and collision avoidance. On this two-dimensional space we calculate where both bodies could be if no one changes course (heading) and then one of us make that change. Collision avoidance IS intercept geometry. Both Fighter and Missile calculate their own collision geometries.
For maneuverable bodies in three dimensional space, we must take into account (V)elocities in all three axes and in (T)ime:
X = [x y z Vx Vy Vz]T or [x y z x-dot y-dot z-dot]T
Where X = state vector, Xb = Bogey, Xf = Fighter and Xm = Missile. We can add i = ICBM, P = Patriot or S = Standard missiles into the mix as well. Plug any two into a matrix and we can have some awfully complex navigation-intercept laws.
This has been 10+ yrs for me from aviation but...In effect...YOU are telling everyone that fixed coordinate system geometry is wrong, that sailors have been using magic all this time to avoid hitting each other, and that the same magic is used by air forces worldwide to shoot each other. Amazing. I have no interest in getting into a mathematical one-upmanship game here. You make a claim and you should support it with external and non-biased sources and so far we have seen nothing to support your claim that it is impossible to predict a flight path. If you want to exaggerate the DF-21's capabilities, make up something that is unique to the weapon, not change physical laws and history to suit.
You have failed -- again -- to support your argument here by showing us a source that explain how in principles, as in contents, are 'rocket' and 'missile' differs. When does a missile achieve orbit? It does not. The section that carries the warhead -- the bus -- is the part that goes into orbit, if that is the intention, and that orbit duration is nothing like a satellite.Ha, that is a first. You again use space rocket principles applying to missile. That shows how much you know about missile. Since when does a missile has to enter a planetary orbit with the exception of maybe X-43A???
An air-air missile must be physically robust because its mission dictate that it must be able to withstand high and sudden transients that involve large angle-of-attack changes. Something called 'aerodynamic bending moments' come with AoA changes and they are greatest in atmosphere.I am not saying it has to maneuver like AAM, but it definitely is more maneuverable than commercial rockets. By using solid fuel the diameter of the rocket body is greatly reduced, thus the casting is more stress resisting as comparing to commercial liquid fuel rockets if their casting are made of the same material and the width of the casting wall are the same.
σc is Hoop Stress and σr is Radial Stress
For example...
Analysis of Credibility of Aerodynamic Loads...
Mass is not physical dimensions. A one-cubic foot block of lead is much heavier than a one-cubic foot block of wood. If we want to increase payload, a desirable mass, given a thrust capability, we must reduce other mass elsewhere, such as the vehicle body itself. That mean a reduced structure and that equate to lower resistance to aerodynamic bending moments. Showing us the stress equations is a distracting tactic. No one can argue against facts. What I do is show the laymen readers applicable and unbiased sources and let them make up their minds instead of trying to impress them with a lot of numbers. You might want to give that a try.In Fig. 5, computed bending moments due to aerodynamic loads at a number of cross sections of the Tu-204's wing, which were specified as design data based on the linear steady model, are compared with results of flight tests. The moments are given in a dimensionless form, being nondimensionalized by dynamic pressure and the characteristic length and area.
But what is NOT factual is your claim that somehow an ICBM is 'more maneuverable' than a satellite launcher. What is 'more maneuverable' ? To what degree ? Why should it need to be 'more maneuverable' ? Where and what are the different points between a 'commercial rocket', your words, and an ICBM ? Only when you provide an external and unbiased source that clearly outlined those differences should we take your arguments seriously.
It is 'Easy' because you made it up. I asked for an example, not your interpretation.
SS-27 is an example I give to you, and you still own me an explanation of how it achieve a flat trajectory using an ideal gravity turn(that is only minimum trust is used to steer the missile for a pitch over, so that it can enter an ideal gravity turn throughout its flight, and the since then the gravity is the only force changing its angular momentum, thus 0 AoA.
Really!!!ICBMs and satellite launchers are alike during the initial rise out of the lower atmosphere. But because a ballistic trajectory is primarily for ground coverage a 'ballistic missile' is a vehicle that continues on a path that must includes more of Earth's gravity than a satellite launcher would.
The purpose of commercial rocket is to send its payload into a planetary orbit, and the purpose of missile is to deliver its payload across great distance by going through a sub-orbital ballistic flightpath. It is true that they are alike in the sense that ICBM could also be used to send its payload into planetary orbit. For example CZ-1 is pretty much identical to DF-4 which it is based on. However the difference in the initial boost phase and angle which it exits the boost phase determines the difference in their ballistic trajectories.
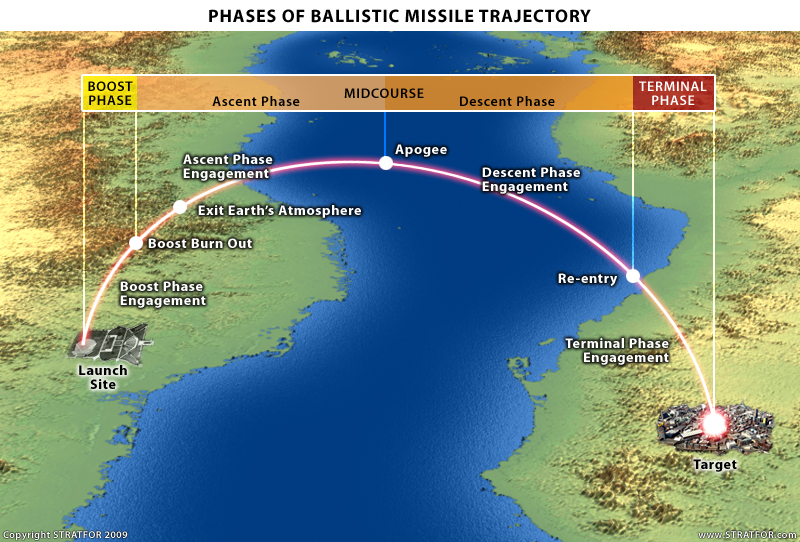

That is correct, that in an ideal gravity turn ascent, the thrust induced steering is at minimum. The duration of the thrust steering could only have one value for its intended trajectory. This is used to maximize the the rocket ability to send its payload to the intended orbit, or the range of ballistic missile. For missile, if it is not aimed at the maximum range for its target, different sets of mixed thrust induced steering and gravity induced steering can produce the same result.In this phrasing:
'After the pitch over is complete the engines are reset to point straight down the axis of the rocket again. This small steering maneuver is the only time during an ideal gravity turn ascent that thrust must be used for purposes of steering.'
A redirection of thrust is initiated to induce a pitch over. The angle and duration of that redirection produce the desired ground coverage. Once the pitch over, which is an angle-of-attack change, is completed and the missile is on the desired heading and in the 'gravity turn' maneuver, thrust is redirected again back to longitudinal alignment, which is another angle-of-attack change in itself. All the while gravity exerts a persistent pull on the entire vehicle.
The word 'ascent' is important because we are trying to send the bus into orbit. The 'ascent' subphase is after the 'boost' phase, which is followed by the mid-course (orbit) phase. The entire phrasing mean that a 'gravity turn' is the ideal maneuver to achieve that ground coverage via ascension to orbit. It also mean ANY gravity turn is an 'ideal gravity turn' regardless if there are any angle-of-attack changes while inside the maneuver.
To put it in a simple prospective, the angle which the missile exit its boost phase determines the ballistic trajectory of the missile. To make everything simple, let's assume the earth is flat and the height of which the missile exits the boost phase is 0, and there is no aerodynamic drag. The speed of which it exits is fixed.
Distance(D) = Initial Velocity(v) * Cos(Angel(a))*Time(t)
Time(t) *Gravity(g)= Sin(Angle(a)) *Velocity(v)
So D = 2*v^2*cos(a)*sin(a)/g = v^2*sin(2a)/g
Since sin(2a)=sin(180-2a), for the same distance it has traveled there can be two values of a with the exception of 0, 45. For example, it can reach the same distance if the angle is 35 degree or 55 degree.
Now you can see how different steering can affect its trajectory even if it is aimed at the same target.
Maths is the simplest and strongest unbiased proof for anyone who understands it. I guess, it is not the case with you.Nice figures but I asked for a source to your claim that target path projections are impossible. Anyone can hack up any math to support his argument and in this publicly accessible forum, the laymen can be misled by non-sourced comments.

Assume the bogey at the time of detection (contact) remain unchanged in this flight, in fixed coordinate system, his would be (Vt,D) where V is the bogey's speed, t is detection time and D is distance between fighter and bogey. Give the fighter's speed as F. Its coordinates would be (Ftsin(h), Ftcos(h)) where h is heading and angle relative to the estimated bogey's flight path. Give the missile's speed as M and substitute for F. Maritime history is full of collisions and collision avoidance. On this two-dimensional space we calculate where both bodies could be if no one changes course (heading) and then one of us make that change. Collision avoidance IS intercept geometry. Both Fighter and Missile calculate their own collision geometries.
For maneuverable bodies in three dimensional space, we must take into account (V)elocities in all three axes and in (T)ime:
X = [x y z Vx Vy Vz]T or [x y z x-dot y-dot z-dot]T
Where X = state vector, Xb = Bogey, Xf = Fighter and Xm = Missile. We can add i = ICBM, P = Patriot or S = Standard missiles into the mix as well. Plug any two into a matrix and we can have some awfully complex navigation-intercept laws.
This has been 10+ yrs for me from aviation but...In effect...YOU are telling everyone that fixed coordinate system geometry is wrong, that sailors have been using magic all this time to avoid hitting each other, and that the same magic is used by air forces worldwide to shoot each other. Amazing. I have no interest in getting into a mathematical one-upmanship game here. You make a claim and you should support it with external and non-biased sources and so far we have seen nothing to support your claim that it is impossible to predict a flight path. If you want to exaggerate the DF-21's capabilities, make up something that is unique to the weapon, not change physical laws and history to suit.
Nice picture, but I don't know how it is going to help you with your case. The case I have shown to you is to prove how the duration acceleration(boost) phase will affect the object path after the acceleration is over. The same principle still applies in your example here. In your example, it is to predict a object's path without any variable changes in the beginning, where as mine a changeable variable is involved.
I never said that it is impossible to predict the flight path of any ballistic missiles, I am only saying that the path can not be determined until all the variables are known to the observer, which is impossible until the boost phase is over. The unknown variables here are duration of the thrust and the thrust used for steering.
It is called sub orbital trajectory.You have failed -- again -- to support your argument here by showing us a source that explain how in principles, as in contents, are 'rocket' and 'missile' differs. When does a missile achieve orbit? It does not. The section that carries the warhead -- the bus -- is the part that goes into orbit, if that is the intention, and that orbit duration is nothing like a satellite.
An air-air missile must be physically robust because its mission dictate that it must be able to withstand high and sudden transients that involve large angle-of-attack changes. Something called 'aerodynamic bending moments' come with AoA changes and they are greatest in atmosphere.
For example...
Analysis of Credibility of Aerodynamic Loads...
Mass is not physical dimensions. A one-cubic foot block of lead is much heavier than a one-cubic foot block of wood. If we want to increase payload, a desirable mass, given a thrust capability, we must reduce other mass elsewhere, such as the vehicle body itself. That mean a reduced structure and that equate to lower resistance to aerodynamic bending moments. Showing us the stress equations is a distracting tactic. No one can argue against facts. What I do is show the laymen readers applicable and unbiased sources and let them make up their minds instead of trying to impress them with a lot of numbers. You might want to give that a try.
But what is NOT factual is your claim that somehow an ICBM is 'more maneuverable' than a satellite launcher. What is 'more maneuverable' ? To what degree ? Why should it need to be 'more maneuverable' ? Where and what are the different points between a 'commercial rocket', your words, and an ICBM ? Only when you provide an external and unbiased source that clearly outlined those differences should we take your arguments seriously.
The stress of the missile due to steering is caused by change of its angular moment of inertia of the missile. Now let's look at the difference here between a rocket and a missile should we.
CZ-2 or DF-5 are both liquid fuel rocket and missile, their diameters are 3.35m and 3.4m, their solid fuel counterpart DF-31's diameter is 2.25m. DF-3 which is also a liquid fuel missile, its diameter is 2.25m, and the solid fuel missile that replace it DF-21 has a body diameter of 1.4m. Now let assume the material for construction of those rocket body is the same, and the thickness of the casting wall is also the same(assuming 0.15m). For the same force that acts on those bodies assuming the load is distributed uniformly , the stress experienced on the body is much less for those with smaller diameter if you apply those numbers to the formula that I gave to you.
What it means is that missiles or rockets with smaller diameters can endure higher g-forces than those with bigger diameters. This also applys to AAM. The reason they can sustain such high g maneuvers besides maybe having better construction materials is that they have much smaller overall diameters.
σc is Hoop Stress and σr is Radial Stress
σc = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] - {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
σr = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] + {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
Last edited:
gambit
PROFESSIONAL

- Joined
- Apr 28, 2009
- Messages
- 28,575
- Reaction score
- 148
- Country
- Location
Har...I owe you zilch. Not only that, what you said above has nothing to do with what you claim to exist: a 'non ideal gravity turn'.SS-27 is an example I give to you, and you still own me an explanation of how it achieve a flat trajectory using an ideal gravity turn(that is only minimum trust is used to steer the missile for a pitch over, so that it can enter an ideal gravity turn throughout its flight, and the since then the gravity is the only force changing its angular momentum, thus 0 AoA.
Yes...Really. You misunderstood what was said about the gravity turn, which tells me you never knew about it in the first place.Really!!!
Which is I why I said that in the lower atmosphere, both behave essentially the same. Now where is that 'non ideal gravity turn' source ?The purpose of commercial rocket is to send its payload into a planetary orbit, and the purpose of missile is to deliver its payload across great distance by going through a sub-orbital ballistic flightpath. It is true that they are alike in the sense that ICBM could also be used to send its payload into planetary orbit. For example CZ-1 is pretty much identical to DF-4 which it is based on. However the difference in the initial boost phase and angle which it exits the boost phase determines the difference in their ballistic trajectories.
Nothing above illustrate how a 'non ideal gravity turn' is created. The fact that you continue to use 'ideal gravity turn' instead of the simple 'gravity turn' tells me you still do not understand how you were in error in the first place. So what we see here is you using a lot of numbers, not to explain anything relevant to your claim, but to hide the fact that you do not know what you are talking about.That is correct, that in an ideal gravity turn ascent, the thrust induced steering is at minimum. The duration of the thrust steering could only have one value for its intended trajectory. This is used to maximize the the rocket ability to send its payload to the intended orbit, or the range of ballistic missile. For missile, if it is not aimed at the maximum range for its target, different sets of mixed thrust induced steering and gravity induced steering can produce the same result.
To put it in a simple prospective, the angle which the missile exit its boost phase determines the ballistic trajectory of the missile. To make everything simple, let's assume the earth is flat and the height of which the missile exits the boost phase is 0, and there is no aerodynamic drag. The speed of which it exits is fixed.
Distance(D) = Initial Velocity(v) * Cos(Angel(a))*Time(t)
Time(t) *Gravity(g)= Sin(Angle(a)) *Velocity(v)
So D = 2*v^2*cos(a)*sin(a)/g = v^2*sin(2a)/g
Since sin(2a)=sin(180-2a), for the same distance it has traveled there can be two values of a with the exception of 0, 45. For example, it can reach the same distance if the angle is 35 degree or 55 degree.
Now you can see how different steering can affect its trajectory even if it is aimed at the same target.
Maths is the simplest and strongest unbiased proof for anyone who understands it. I guess, it is not the case with you.
Until ? That is what radar is for. Radar will tell us target heading, speed, altitude and aspect angle with respect to us. Everything we need for fixed coordinates collision intercept.Nice picture, but I don't know how it is going to help you with your case. The case I have shown to you is to prove how the duration acceleration(boost) phase will affect the object path after the acceleration is over. The same principle still applies in your example here. In your example, it is to predict a object's path without any variable changes in the beginning, where as mine a changeable variable is involved.
I never said that it is impossible to predict the flight path of any ballistic missiles, I am only saying that the path can not be determined until all the variables are known to the observer, which is impossible until the boost phase is over. The unknown variables here are duration of the thrust and the thrust used for steering.
This still does not answer the question of why SHOULD an ICBM be more structurally robust than a satellite launcher. You already admitted that in the boost phase, both are essentially the same. Further, an ICBM is usually launched in home territory, its flight will be mainly for altitude, by the burn-out time of 3-4 min the most important part of the missile will be 6-7 km/s and far above the operating altitude of any fighters, hostile or not. Any horizontal travel that could potentially take the missile into enemy controlled territory would be negated by that burn-out altitude. So what need is there for an ICBM to be any more structurally robust than what is necessary, or more than a satellite launcher, when being so will cost us payload capability ?The stress of the missile due to steering is caused by change of its angular moment of inertia of the missile. Now let's look at the difference here between a rocket and a missile should we.
CZ-2 or DF-5 are both liquid fuel rocket and missile, their diameters are 3.35m and 3.4m, their solid fuel counterpart DF-31's diameter is 2.25m. DF-3 which is also a liquid fuel missile, its diameter is 2.25m, and the solid fuel missile that replace it DF-21 has a body diameter of 1.4m. Now let assume the material for construction of those rocket body is the same, and the thickness of the casting wall is also the same(assuming 0.15m). For the same force that acts on those bodies assuming the load is distributed uniformly , the stress experienced on the body is much less for those with smaller diameter if you apply those numbers to the formula that I gave to you.
What it means is that missiles or rockets with smaller diameters can endure higher g-forces than those with bigger diameters. This also applys to AAM. The reason they can sustain such high g maneuvers besides maybe having better construction materials is that they have much smaller overall diameters.
σc is Hoop Stress and σr is Radial Stress
σc = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] - {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
σr = [(pi*ri^2 - po*ro^2) / (ro^2 - ri^2)] + {ri^2*ro^2*(po - pi) / [r^2*(ro^2 - ri^2)]}
Once again...More numbers to obfuscate the fact that you cannot support your argument.
topjumper
FULL MEMBER

- Joined
- Feb 18, 2010
- Messages
- 383
- Reaction score
- 0
For maneuverable bodies in three dimensional space, we must take into account (V)elocities in all three axes and in (T)ime:
X = [x y z Vx Vy Vz]T or [x y z x-dot y-dot z-dot]T
Where X = state vector, Xb = Bogey, Xf = Fighter and Xm = Missile. We can add i = ICBM, P = Patriot or S = Standard missiles into the mix as well. Plug any two into a matrix and we can have some awfully complex navigation-intercept laws.
This has been 10+ yrs for me from aviation but...In effect...YOU are telling everyone that fixed coordinate system geometry is wrong, that sailors have been using magic all this time to avoid hitting each other, and that the same magic is used by air forces worldwide to shoot each other.
Ok I don't mean to butt in here as there are too many technicalities that I do not know about, but just to dwell a little on the maths here,
let's say x is a [6x1] vector for ICBM as you have explained, y is the [6x1] vector for the intercepting missile , A is a [6x6] configuration matrix that will be used to determine y given x (once it is launched and detected): y = Ax.
However this model only works if the velocity of the ICBM is constant or known as in the case of air-traffic or shipping lane traffic control etc, it doesn't take into account of the ICBM's acceleration as we know it maneuvers itself, so we'd need to have at least x = [X, X-dot, X-dot dot] (X for space vector), but the last three elements of x is unknown and you essentially have an under-determined linear system that doesn't have a definitive solution. Unless the intercepting missile is capable of constantly detecting and calculating the incoming missile's acceleration and adjusting itself on the fly (no pun intended), are the current missiles sophisticated and powerful enough to do this?
Thomas
PROFESSIONAL

- Joined
- Jul 22, 2009
- Messages
- 2,688
- Reaction score
- 0
Unless the intercepting missile is capable of constantly detecting and calculating the incoming missile's acceleration and adjusting itself on the fly (no pun intended), are the current missiles sophisticated and powerful enough to do this?
Yes they are!
One aspect of the Aegis BMD system is it can constantly update the missile while in flight.
RIM-161 SM-3 (AEGIS Ballistic Missile Defense)
"if the third stage requires a course correction for an intercept, the rocket motor begins the second pulse burn. Upon completion of the second pulse burn, the IR seeker is calibrated and the KW ejects. The KW possesses its own attitude control system and guidance commands are acted upon by a solid divert propulsion system. The IR seeker acquires the target. Tracking information is continuously transmitted to the guidance assembly which controls the divert propulsion system.
Aegis BMD is capable of using data from space-based sensors or cues from other elements of the BMDS, however external cues and sensor data is not required for Aegis BMD. The system is designed to be capable of autonomous (self-contained) operations for detection, tracking, and engagement of ballistic missile targets or reporting ballistic missile track data to other elements of the BMDS."
gambit
PROFESSIONAL

- Joined
- Apr 28, 2009
- Messages
- 28,575
- Reaction score
- 148
- Country
- Location
That is what radar is for. There are two target resolutions here and we are talking about terminal defense for now. The first radar target resolutions come from the defense main radar. The second is from the interceptor missile itself. Target resolutions are: heading, speed, altitude and aspect angle.Ok I don't mean to butt in here as there are too many technicalities that I do not know about, but just to dwell a little on the maths here,
let's say x is a [6x1] vector for ICBM as you have explained, y is the [6x1] vector for the intercepting missile , A is a [6x6] configuration matrix that will be used to determine y given x (once it is launched and detected): y = Ax.
However this model only works if the velocity of the ICBM is constant or known as in the case of air-traffic or shipping lane traffic control etc, it doesn't take into account of the ICBM's acceleration as we know it maneuvers itself, so we'd need to have at least x = [X, X-dot, X-dot dot] (X for space vector), but the last three elements of x is unknown and you essentially have an under-determined linear system that doesn't have a definitive solution. Unless the intercepting missile is capable of constantly detecting and calculating the incoming missile's acceleration and adjusting itself on the fly (no pun intended), are the current missiles sophisticated and powerful enough to do this?
Similar threads
- Replies
- 0
- Views
- 239
- Replies
- 0
- Views
- 179
- Replies
- 0
- Views
- 277
- Replies
- 0
- Views
- 353

