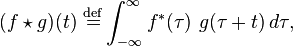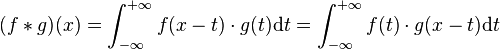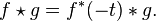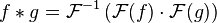Picdelamirand-oil
PROFESSIONAL

- Joined
- Feb 14, 2016
- Messages
- 462
- Reaction score
- 5
- Country
- Location
1) TDOA (Multilateration - Wikipedia, the free encyclopedia)
If a pulse is emitted from a platform, it will generally arrive at slightly different times at two spatially separated receiver sites, the TDOA being due to the different distances of each receiver from the platform. In fact, for given locations of the two receivers, a whole set of emitter locations would give the same measurement of TDOA. Given two receiver locations and a known TDOA, the locus of possible emitter locations is one half of a two-sheeted hyperboloid.

Fig 1. A two-sheeted hyperboloid
In simple terms, with two receivers at known locations, an emitter can be located onto a hyperboloid.[1] Note that the receivers do not need to know the absolute time at which the pulse was transmitted – only the time difference is needed.
Consider now a third receiver at a third location. This would provide a second TDOA measurement and hence locate the emitter on a second hyperboloid. The intersection of these two hyperboloids describes a curve on which the emitter lies.
If a fourth receiver is now introduced, a third TDOA measurement is available and the intersection of the resulting third hyperboloid with the curve already found with the other three receivers defines a unique point in space. The emitter's location is therefore fully determined in 3D.
In practice, errors in the measurement of the time of arrival of pulses mean that enhanced accuracy can be obtained with more than four receivers. In general, N receivers provide N − 1 hyperboloids. When there are N > 4 receivers, the N − 1 hyperboloids should, assuming a perfect model and measurements, intersect on a single point. In reality, the surfaces rarely intersect, because of various errors. In this case, the location problem can be posed as an optimization problem and solved using, for example, a least squares method or an extended Kalman filter.
Additionally, the TDOA of multiple transmitted pulses from the emitter can be averaged to improve accuracy.
The accuracy also improves if the receivers are placed in a configuration that minimizes the error of the estimate of the position.
The emitting platform may, or may not, cooperate in the multilateration surveillance processes.
2 Interferometry
The measurement of a phase is a distance measurement: 2pi correspond to the wavelength, In other words approximately 3 cm in the band X. The problem is that it is a precise distance measurement modulo the wavelength.
The direction of a transmitter can be calculated by measuring the time delay between the arrival of the signal on two antennas with a known distance. Indeed the locus of points that generate the same delay is hyperbole whose foci are the two antennas. We then assimilates the hyperbole to their assymptotes because in general the transmitter is far.
For measuring a delay we can make correlations between the signals received by an antenna and that received by the other, the signals are shifted in time by an antenna relative to another until one has the correlation. The time that has allowed this correlation is the offset of the arrival of the signal from both antennas.
We have our hyperbole, that is, 4-way, but if we do the same treatment with another pair of antennas we have 4 other directions and if we have well designed geometry of the two pairs only one direction shall be common to two doublets. So we have the direction of the transmitter. This is the DTOA treatment described in more detail in the first paragraph.
But it is not accurate. To improve accuracy we measure the signal phase to the arrival of the two antennas. We have seen that this was a distance measuring modulo the wavelength, the delay is also a measurement of distance by multiplying by the speed of light. The assembly of the two measurements provides a measure of precise distance. It can be converted into measure precise delay.
If the delay is accurately measured and the distance between the two antennas is also known precisely, we can deduce a precise direction of the transmitter. Antennas have known positions built, but they should not "move" with respect to the other, so interferometry is NOT recommended if the antennas are wingtip. It takes place on a rigid part of the plane if you do not want to lose the advantage of the accuracy of the measured delay.
If a pulse is emitted from a platform, it will generally arrive at slightly different times at two spatially separated receiver sites, the TDOA being due to the different distances of each receiver from the platform. In fact, for given locations of the two receivers, a whole set of emitter locations would give the same measurement of TDOA. Given two receiver locations and a known TDOA, the locus of possible emitter locations is one half of a two-sheeted hyperboloid.

Fig 1. A two-sheeted hyperboloid
In simple terms, with two receivers at known locations, an emitter can be located onto a hyperboloid.[1] Note that the receivers do not need to know the absolute time at which the pulse was transmitted – only the time difference is needed.
Consider now a third receiver at a third location. This would provide a second TDOA measurement and hence locate the emitter on a second hyperboloid. The intersection of these two hyperboloids describes a curve on which the emitter lies.
If a fourth receiver is now introduced, a third TDOA measurement is available and the intersection of the resulting third hyperboloid with the curve already found with the other three receivers defines a unique point in space. The emitter's location is therefore fully determined in 3D.
In practice, errors in the measurement of the time of arrival of pulses mean that enhanced accuracy can be obtained with more than four receivers. In general, N receivers provide N − 1 hyperboloids. When there are N > 4 receivers, the N − 1 hyperboloids should, assuming a perfect model and measurements, intersect on a single point. In reality, the surfaces rarely intersect, because of various errors. In this case, the location problem can be posed as an optimization problem and solved using, for example, a least squares method or an extended Kalman filter.
Additionally, the TDOA of multiple transmitted pulses from the emitter can be averaged to improve accuracy.
The accuracy also improves if the receivers are placed in a configuration that minimizes the error of the estimate of the position.
The emitting platform may, or may not, cooperate in the multilateration surveillance processes.
2 Interferometry
The measurement of a phase is a distance measurement: 2pi correspond to the wavelength, In other words approximately 3 cm in the band X. The problem is that it is a precise distance measurement modulo the wavelength.
The direction of a transmitter can be calculated by measuring the time delay between the arrival of the signal on two antennas with a known distance. Indeed the locus of points that generate the same delay is hyperbole whose foci are the two antennas. We then assimilates the hyperbole to their assymptotes because in general the transmitter is far.
For measuring a delay we can make correlations between the signals received by an antenna and that received by the other, the signals are shifted in time by an antenna relative to another until one has the correlation. The time that has allowed this correlation is the offset of the arrival of the signal from both antennas.
We have our hyperbole, that is, 4-way, but if we do the same treatment with another pair of antennas we have 4 other directions and if we have well designed geometry of the two pairs only one direction shall be common to two doublets. So we have the direction of the transmitter. This is the DTOA treatment described in more detail in the first paragraph.
But it is not accurate. To improve accuracy we measure the signal phase to the arrival of the two antennas. We have seen that this was a distance measuring modulo the wavelength, the delay is also a measurement of distance by multiplying by the speed of light. The assembly of the two measurements provides a measure of precise distance. It can be converted into measure precise delay.
If the delay is accurately measured and the distance between the two antennas is also known precisely, we can deduce a precise direction of the transmitter. Antennas have known positions built, but they should not "move" with respect to the other, so interferometry is NOT recommended if the antennas are wingtip. It takes place on a rigid part of the plane if you do not want to lose the advantage of the accuracy of the measured delay.